Given:
The distance covered while travelling with the current is, d(1) = 60 miles.
The distance covered while travelling against the current is, d(2) = 10 miles.
The speed of the current is, s(w) = 5 mph.
The objective is to find the rate of team s(t) in still water.
Step-by-step explanation:
It is given that, the time taken during the direction of current and against the current is same.
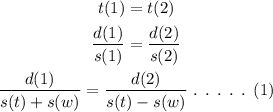
On plugging the given values in equation (1),
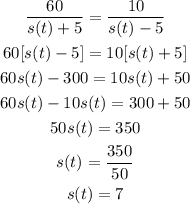
Hence, the rate of team still in the water = 7 mph.