Question

Determine whether the graphs of the given equations are parallel, perpendicular, or neither x-5y=-4y=2x-8

Answer 1

The lines are neither parallel nor perpendicular

Here, we want to determine the relationship between the two lines

We rewrite the first equation in the standard form of;

`y\text{ = mx + b}`

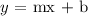
m is the slope and b is the y-intercept

For the line, we have;

`\begin{gathered} 5y\text{ = x+4} \\ y\text{ = }(x)/(5)+(4)/(5) \end{gathered}`

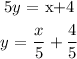
The value of the slope is 1/5 and as such, it is not equal to that of the first line which means they cannot be parallel

Also, the product of the slopes is not equal to -1 which means the two lines are not perpendicular too