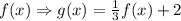Question

how do you know whether something is a vertical or horizontal stretch or shrink? how do you know if it's horizontal or vertical?

Answer 1

An horizontal compression (or stretch) acts on the horizontal axis, which is related with variable x. Then, we have

Now, a vertical compression (or stretch) acts on the vertical axis, which is related with variable y (or f(x)). Then, we have

If we have the following expression:

`g(x)=(1)/(3)x^2+2`

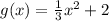
the parent function is

`f(x)=x^2`

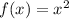
so, in order to get g(x) from f(x), we need a translation up 2 units and a vertical stretch by 1/3, that is,

`f(x)\Rightarrow g(x)=(1)/(3)f(x)+2`