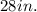Question

Need help understanding how to do problems like this. Is there like a general strat?

Answer 1

To solve this problem, we will use the following diagram as reference:

Using the Pythagorean theorem, we get that ( we will omit the units to simplify the calculations):

`100^2=(x+68)^2+x^2.`

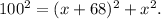
Therefore:

`\begin{gathered} 100^2=x^2+136x+68^2+x^2, \\ 2x^2+136x+68^2-100^2=0, \\ 2x^2+136x-5376=0. \end{gathered}`

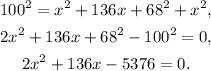
Using the quadratic formula, we get:

`x=\frac{-136\pm\sqrt[]{136^2-4(2)(-5376)}}{2(2)}.`

Simplifying the above result, we get:

`\begin{gathered} x_1=28, \\ x_2=-96. \end{gathered}`

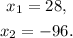
Since, the negative solution has no meaning in the context of the problem, x=28 in.

Answer:

`28in\text{.}`