Given:

To find:
The derivative.
Step-by-step explanation:
a) Using the quotient rule,
![\begin{gathered} y^(\prime)=((x-a)(d)/(dx)(x^2-a^2)-(x^2-a^2)(d)/(dx)(x-a))/((x-a)^2) \\ =((x-a)(2x)-(x^2-a^2))/((x-a)^2) \\ =((x-a)(2x)-(x-a)(x+a))/((x-a)^2)\text{ \lbrack Since, }x^2-a^2=(x+a)(x-a)] \\ =((x-a)[2x-(x+a)])/((x-a)^2) \\ =((x-a)(x-a))/((x-a)^2) \\ y^(\prime)=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/464xz3mw2pmx2r3bgaaoldajaqmv5a7opf.png)
b)
By expanding the product and simplifying the quotient, we get
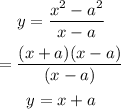
Differentiating with respect to x we get,
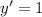
The part (a) answer and the part (b) answer are the same.
Hence verified.
Final answer:
The derivative for the given problem is 1.