Question

The revenue for selling x units of a product is R = 150x. The cost of producing x units is C = 125x + 800. For what values of x will this product generate a profit?

Answer 1

To solve the exercise you know that the income from selling x units of the product must be greater than the cost of producing these units of the product, then

`\begin{gathered} R(x)>C(x) \\ 150x>125x+800 \end{gathered}`

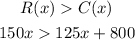
Now, you can solve the inequality

`\begin{gathered} 150x>125x+800 \\ \text{ Subtract 125x from both sides of the inequality} \\ 150x-125x>125x+800-125x \\ 25x>800 \\ \text{ Divide by 25 from both sides of the inequality} \\ (25x)/(25)>(800)/(25) \\ x>32 \end{gathered}`

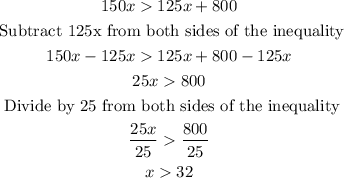
Therefore, for values ​​of x greater than 32, this product will generate a profit.