Question

I need help with these questions it's to find perimeter.

Answer 1

EXPLANATION

9) We can see that this is an Equilateral Triangle, so the perimeter is given by the following equation:

`\text{Perimeter}=\text{base}+\text{leg}1+\text{leg}2`

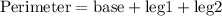
We have that the height is equal to 4sqrt(15), but we don't know the base, so we can get this by applying the Law of Sines over the inside right triangle:

Law of Sines:

`(a)/(\sin a)=(b)/(\sin b)`

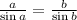
Let's call x to the unknown leg:

`(x)/(\sin 90)=\frac{4\sqrt[]{15}}{\sin 60}`

Isolating x:

`x=(\sin90)/(\sin60)4\sqrt[]{15}=\frac{1}{\frac{\sqrt[]{3}}{2}}4\sqrt[]{15}=\frac{2}{\sqrt[]{3}}4\sqrt[]{15}=2\cdot4\frac{\sqrt[]{3}\cdot\sqrt[]{5}}{\sqrt[]{3}}`

Simplifying terms:

`x=8\sqrt[]{5}`

Now, we know that both legs are equal to 8*sqrt(5) because this is an Equilateral Triangle and the base is also the same.

`\text{Base }=legs=8\sqrt[]{5}`

Finally, the Perimeter is:

`\text{Perimeter}=8\sqrt[]{5}+8\sqrt[]{5}+8\sqrt[]{5}=3\cdot(8\sqrt[]{5})=24\sqrt[]{5}`

The Perimeter is:

`\text{Perimeter}=24\sqrt[]{5}`