Question

consider the line 8x - 7y = 2.What is the slope of a line perpendicular to this line?What is the slope of a line parallel to this line?

Answer 1

We have the following one-line equation:

`8x-7y=2`

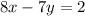
We must find the slope of a perpendicular line and a line parallel to the one described in this function, to do this it is necessary to first identify the slope of our line.

So first we leave the equation of the line in the standard form of the line.

`y=mx+b`

So we clear "y" from our equation from the line

`\begin{gathered} 8x-7y=2 \\ 7y=8x-2 \\ y=(8)/(7)x-(2)/(7) \end{gathered}`

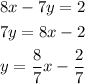
where "m" is the slope, in this case:

`m=(8)/(7)`

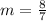
Perpendicular line

The equation of a perpendicular line must have a slope that is the negative reciprocal of the original slope, i.e. the product of the slopes is -1.

`\begin{gathered} -1=m\cdot m_(per) \\ -1=(8)/(7)\cdot m_(per) \\ m_(per)=-(1)/((8)/(7)) \\ m_(per)=-(7)/(8) \end{gathered}`

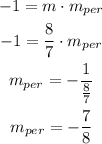
In conclusion, the slope for a line perpendicular is -7/8

Parallel line

The slope between parallel lines is always the same, i.e. their slope is the same.

`m_(par)=(8)/(7)`

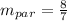
In conclusion, the slope for a line parallel is 8/7