Question

Assume the tabLe is exponential There was a release of European wild rabbits in Victoria, Australia in December 1858. without natural predators, the population grew. Round to the nearest whole number

Answer 1

The population of rabbits (P) can be expressed with an exponential model of the form:

`P=a* e^(b* t)`

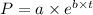
Then, we need to find the values of a and b in order to calculate the population at the time t.

Let's take the population at time t1 to be P1 and the population at time t2 to be P2. then:

`\begin{gathered} P1=a* e^(b* t1) \\ P2=a* e^(b* t2) \end{gathered}`

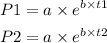
By taking the ratio of P1 to P2, we get:

`\begin{gathered} (P1)/(P2)=(a* e^(b* t1))/(a* e^(bt1)) \\ (P1)/(P2)=(a)/(a)*(e^(b* t1))/(e^(bt*1)) \\ (P1)/(P2)=(a)/(a)* e^(b* t1-b* t2) \\ (P1)/(P2)=e^(b*(t1-t2)) \end{gathered}`

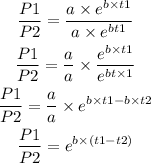
We can solve for b by taking the natural logarithm on both sides of this expression:

`\begin{gathered} (P1)/(P2)=e^(b*(t1-t2)) \\ \ln ((P1)/(P2))=\ln (e^(b*(t1-t2))) \\ \ln ((P1)/(P2))=b*(t1-t2)\ln (e^{}) \\ b=(\ln((P1)/(P2)))/((t1-t2)) \end{gathered}`

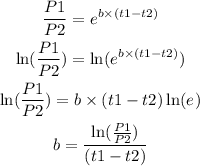
By taking the first and the second row of the table, we can calculate b like this:

`b=(\ln ((250)/(375)))/((12-13))\approx0.4`

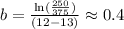
Now that we know the value of b, we only need to calculate a, we can do it like this:

`\begin{gathered} P=a* e^(b* t) \\ a=(P)/(e^(b* t)) \end{gathered}`

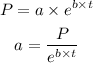
Taking the data of the third row, we get:

`a=(563)/(e^(0.4*14))\approx1.92`

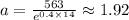
Then, for the time 15 and 16, we get:

`\begin{gathered} P=1.92* e^(0.4*15)\approx844.5 \\ P=1.92* e^(0.4*16)\approx1266.75 \end{gathered}`