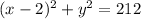Answer::
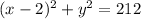
Explanation:
Given the endpoints of the diameter of a circle, we are required to write the equation of the circle.
The standard form of the equation of a circle is given as:
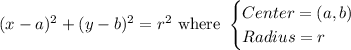
So, we need to find two things, the center, and the radius.
Center
The center of the circle is the midpoint of the diameter.
Given the endpoints as: (16, -4) and (-12,4)
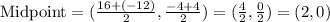
The center, (a,b)=(2,0).
Radius
The radius is the distance between the center, (2,0) and one of the endpoints of the diameter.
Using the distance formula, we find the distance between (2,0) and (16,-4).
![\begin{gathered} Distance=√((x_2-x_1)^2+(y_2-y_1)^2) \\ =\sqrt[]{(16-2)^2+(-4-0)^2}=\sqrt[]{(14)^2+(-4)^2}=\sqrt[]{212} \\ \implies\text{Radius}=√(212) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6ox0fddoaev2gu83c0pw7np7ydkldsq82w.png)
Substitute these values into the equation given earlier:
![\begin{gathered} (x-2)^2+(y-0)^2=\sqrt[]{212}^2\text{ where }\begin{cases}Center,(a,b)=(2,0) \\ Radius,r=\sqrt[]{212}\end{cases} \\ (x-2)^2+y^2=212 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/lv8ej82u8raqs6is03iyiikdn9fthymfkj.png)
The equation of the circle is: