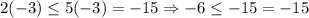Question

I need help solving this multi step compound inequality. this was all the information they gave for the equation on my assignment.

Answer 1

We will ahve the following:

`2x\le5x=-15`

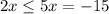
This problem has the solution.

`\Rightarrow2x+15\le5x+15=0\Rightarrow1\le(5x+15)/(2x+15)=0`

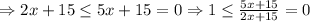
After this point you can reduce further.

`1\le(5x+15)/(2x+15)=0`

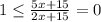
We would need a value of "x" that makes "5x + 15" = 0 [We cannot have that "2x + 15 = 0" since it would be undetermined] so:

`\rightarrow5x+15=0\rightarrow5x=-15\rightarrow x=-3`

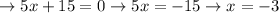
Now, when we replace this value:

`2(-3)\le5(-3)=-15\Rightarrow-6\le-15=-15`