Our approach is the binomial probability model.
Let p represent the probability of obtaining a yellow ball.
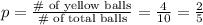
Let q represent the probability of obtaining a non-yellow ball, i.e, a white ball.

Binomial probability
To get r successes in n trial is:
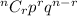
where:
n = number of balls chosen at random
r = number of yellow balls to be selected
n- r = number of white balls to be selected
Applying, we get:
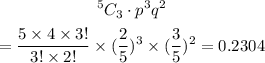
The probability that he will select 3 yellow balls and 2 white balls is 0.230