Question

Determine whether the lines are passing through the pairs of points are parallel, perpendicular, or neither.

Answer 1

Given:

`\begin{gathered} L_1:(1,-3),(4,12) \\ L_2:(3,4),(13,2) \end{gathered}`

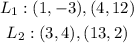
Required:

Find whether the lines passing through the pairs of points are parallel, perpendicular, or neither.

Step-by-step explanation:

The slope of the line

`L_1`
`\begin{gathered} m_1=(12-(-3))/(4-1) \\ =(15)/(3) \\ =5 \end{gathered}`

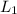
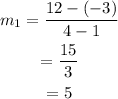
The slope of the line

`L_2`
`\begin{gathered} m_2=(2-4)/(13-3) \\ =(-2)/(10) \\ =-(1)/(5) \end{gathered}`

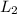
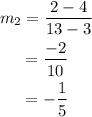
The product of the slopes is:

`\begin{gathered} m_1m_2=5*-(1)/(5) \\ =-1 \end{gathered}`

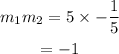
The product of the slope is -1 so the lines will be perpendicular.

Final Answer:

The second option is the correct answer.