Question

7) Sia owns a candy store, and she wants to mix gummy worms worth $3 per pound with gummy bears worth $1.50 per pound to make 30 pounds of a mixture worth $63.00. (5pts each) a) Analyze and set-up a system of equations for this mixture (quantity-value system). b) Solve this system of equations to determine how many pounds of each of candy Sia should use for this mixture.

Answer 1

`\begin{gathered} a)\text{ w + b = 30} \\ 3w\text{ + 1.5b = 63} \\ \\ b)\text{ 18 gummy bears and 12 gummy worms} \end{gathered}`

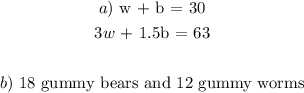
where w is the number of gummy worms and b is the number of gummy bears

Here, we want to set up equations

Let the number of pounds of gummy worms be w and the number of pounds of gummy bears be b

From the question, we have that the sum of all is 30

Thus, we have it that;

`w\text{ + b = 30 }\ldots\ldots\ldots....\ldots..(i)_{}`

Now, for w pounds of gummy worms at a cost of $3 per pound, we have the cost here as 3 * w = $3w

Secondly, for b pounds of gummy bears at a cost of $1.5 per pound, we have the cost as 1.5 * b = $1.5b

The cost of both gives;

`3w\text{ + 1.5b = 63 }\ldots\ldots\ldots\ldots\ldots\ldots..(ii)`

Thus, we have the system of equations as follows;

`\begin{gathered} w\text{ + b = 30} \\ 3w\text{ + 1.5b = 63} \\ \text{Multiply equation i by 3 and i}i\text{ by 1} \\ 3w\text{ + 3b = 90} \\ 3w\text{ + 1.5b = 63} \\ \text{Subtract equation }ii\text{ from i} \\ 3b-1.5b\text{ = 90-63} \\ 1.5b\text{ = 27} \\ b\text{ = }(27)/(1.5) \\ b\text{ = 18} \\ \\ \text{From equation i;} \\ w\text{ + b = 30} \\ w\text{ = 30-b} \\ w\text{ = 30-18} \\ w\text{ = 12} \end{gathered}`