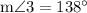Step-by-step explanation:
Consider the following picture:
When two parallel lines are cut by a transversal, the pairs of angles formed on the inside of one side of the transversal are called consecutive interior angles. Now, the pair of consecutive interior angles are supplementary. Thus, we get the following equation:
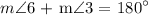
applying the data of the problem, the previous equation is equivalent to:
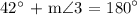
solving for angle 3, we get:
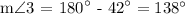
now, remember that vertical angles are equal, thus we get the following equation:
![m\angle1\text{ =m}\angle3=138^(\circ)^^]()
thus, we can conclude that the correct answer:
Answer:
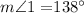
and