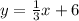Question

Choose the slope intercept equation of the line that passes through the point (-6,4) and is parallel to y= 1/3x-4

Answer 1

`y=(1)/(3)x+6`

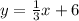
Step-by-step explanation

If two lines are parallel then they have the same slope. Therefore, the slope of the line we want to find is 1/3. In the slope-intercept form, we have:

`y=(1)/(3)x+b`

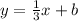
To find the y-intercept b we have to replace x and y by the given point (-6, 4) and solve for b:

`\begin{gathered} 4=(1)/(3)(-6)+b \\ 4=-2+b \\ b=4+2 \\ b=6 \end{gathered}`

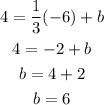
The equation of the line in slope-intercept form is:

`y=(1)/(3)x+6`