Answer
The mole fraction of O2 in the tank = 0.101
The partial pressure of O2 in the tank = 0.264 atm
Step-by-step explanation
Given:
Volume, V = 12.5 L
Temperature, T = 25 °C = (25 + 273.15 K) = 298.15 K
Mass of helium = 24.2 g
Mass of O2 = 4.32 g
Step-by-step solution:
The first step is to calculate the total pressure. The total pressure can be calculated using the ideal gas equation.
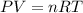
n is the total moles in the container and can be calculated by converting the grams of helium and O2 to moles by taking their grams and dividing by their molar masses:
24.2 grams Neon x (1 mol Neon / 20.18 g Neon) = 1.199 mol Neon
4.32 grams Oxygen x (1 mol Oxygen / 31.998 g O2) = 0.135 mol Oxygen
Total moles = 1.199 + 0.135 = 1.334 mol
Now, we can solve for the total pressure using the equation above.
Putting V = 12.5 L; T = 298.15 K; n = 1.334 mol and R = 0.0821 L atm / mol K.
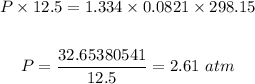
The total pressure in the tank = 2.61 atm.
The mole fraction of O2 in the tank:
The mole fraction of O2 in the tank can be calculated using
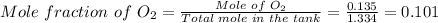
The mole fraction of O2 in the tank = 0.101
The partial pressure of O2 in the tank:
The partial pressure of O2 in the tank in the tank can be calculated using
Partial fraction of O2 = mole fraction of O2 x total pressure
Putting mole fraction of O2 = 0.101, and total pressure = 2.61 atm
Partial fraction of O2 = 0.101 x 2.61 atm = 0.264 atm
The partial pressure of O2 in the tank = 0.264 atm