Question

A +10.24 nC charge is located at (0,11.44) cm and a -3.63 nC charge is located (4.1, 0) cm. Where would a -15.03 nC charge need to be located in order that the electric field at the origin be zero? Express your answer, in cm, as the magnitude of the distance of q3 from the origin.

Answer 1

Our situation is the following:

We want the electric field at (0,0) to be 0. First, let us write how it is at the current moment. This can be achieved by summing the influence of both particles. This gives us the following:

`\vec{E}_((0,0))=\vec{E}_((x,0))+\vec{E}_((0,y))=(kq_((x,0)))/(x^2)\hat{x}+(kq_((0,y)))/(y^2)\hat{y}`

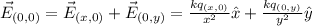
By applying our values to the equation, the current electric field on the origin can be written as:

`\vec{E}=(k*3.63*10^(-9))/((4.1*10^(-2))^2)\hat{x}-(k*10.24*10^(-9))/((11.44*10^(-2))^2)\hat{y}=19434.8602\hat{x}-7041.90914\hat{y}`

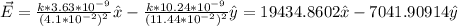
The magnitude of the vector can be written as the root of the quadratic sum of its components, as you can see in the following drawing:

Thus, the magnitude of E is:

`|\vec{E}|\text{ = }\sqrt[\placeholder{⬚}]{19434.8602^2+7041.90914^2}=20671.29109`

With the magnitude of E in hands, we know that we would need to place the particle q3 in a distance, such that the electric field generated by this particle will nullify the one produced by the other particles:

Given we know its value, we can find out the distance by using the same formula. We know that:

`20671.29109=(k*15.03*10^(-9))/(d^2)`

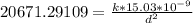
Therefore:

`d=\sqrt[\placeholder{⬚}]{(k*15.03*10^(-9))/(20671.29109)}=0.08089m`

Then, our final answer is d=8.089cm