Question

Finding the asymptotes of a rational function: Linear over linear

Answer 1

`f(x)=(-8x+13)/(2x+9)`

Vertical asymptote at x=a if the denominator is zero at x=a and the numerator isn't zero at x=a

Equal the denominator to zero and solve x:

`\begin{gathered} 2x+9=0 \\ 2x=-9 \\ x=-(9)/(2) \\ \end{gathered}`

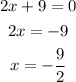
Prove if x=-9/2 makes the numerator equal to 0:

`-8(-(9)/(2))+13=-(72)/(2)+13=-23`

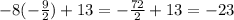
As the value x=-9/2 doesn't make the numerator be equal to zero the function has a vertical asymptote in x=-9/2

_______________

`f(x)=\frac{ax^n+\text{.}\ldots}{bx^m+\cdots}`

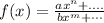
Numerator and denominator have the same largest exponent. Then, the line y=a/b is the horizontal asymptote:

`\begin{gathered} x=(-8)/(2) \\ \\ x=-4 \end{gathered}`

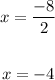
Then, the given function has the next asymptotes:

Vertical asymptote: y= -9/2 (in red)

Horizontal asymptote: x= -4 (in blue)