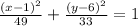Step-by-step explanation
The equation of an ellipse looks like this:
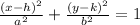
Where its center is located at (h,k), its vertices are located at (h+a,k) and (h-a,k) and its foci are located at (h+c,k) and (h-c,k) with c² = a² - b². Since we have the center, a vertex and a focus of the ellipse we can use them to find a, b, h and k.
We are told that the center of this ellipse is located at (1,6) which means that:
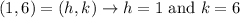
So for now we have:
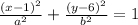
Now it's important to know that the focal length c is always a positive number. We know that one of the focus of the ellipse is located at (-3,6). Since the expression for the foci of the ellipse are (h+c,k) and (h-c,k) if we take (h,k)=(1,6) we obtain:
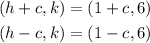
One of these two has to be equal to (-3,6). The correct one will be that with c>0. Then we get:
![\begin{gathered} (1+c,6)=(-3,6)\Rightarrow1+c=-3\Rightarrow c=-3-1=-4\Rightarrow c<0 \\ (1-c,6)=(-3,6)\operatorname{\Rightarrow}1-c=-3\operatorname{\Rightarrow}c=3+1=4\operatorname{\Rightarrow}c>0 \end{gathered}]()
So as you can see the correct value of c is 4. Then we take the equation of c:
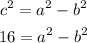
So we have an equation for a and b. We can use the coordinates of the vertex given by the question (8,6). We know that the vertices are located at (h+a,k) and (h-a,k). We can assume that a>0 without problems and we repeat the same calculations that we made for the focus and c but for the vertex (8,6) and a:
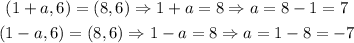
We take the first value because it's positive and we get a=7. Now that we have a we can find b using the equation of c:
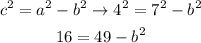
We add b² to both sides and we substract 16 from both sides:
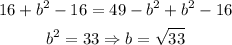
So we have found a, b, h and k which means that we can write the equation of the ellipse.
Answer
Then the answer is: