Question

As grain is being unloaded from a freight car, the rising pile is in the shape of a cone. As more and more grain pours onto the pile, the pile grows, but the cones at different stages are always similar. After 1 hour, the height of the cone is 5 feet and the radius of the base is 9 feet. After 3 hours, the height is 12 feet. How much area on the ground does the pile cover at this point?

Answer 1

`\begin{equation*} 1465.74ft^2 \end{equation*}`

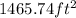
Step-by-step explanation

We want to find the area on the ground that the pile covers at that point.

To do this, we have to first find the radius of the base of the cone at the point where its height is 12 feet and then, find the area of the circle formed by the base of the cone.

Since the cones at different stages are similar, it implies that the ratio of their radii and heights are proportional.

Therefore, we have the following proportion:

`\begin{gathered} 5ft=9ft \\ 12ft=xft \end{gathered}`

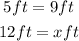
Cross-multiply and solve for r:

`\begin{gathered} r*5=12*9 \\ r=(12*9)/(5) \\ r=21.6ft \end{gathered}`

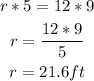
That is the radius of the base of the cone when its height is 12 feet.

Hence, the area on the ground that the pile covers is:

`\begin{gathered} A=\pi r^2 \\ A=\pi *21.6^2 \\ A=1465.74ft^2 \end{gathered}`

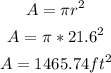
That is the answer.