Question

How to find the volume of a pentagon without the apothem

Answer 1

Volume = 928.8 in³

Step-by-step explanation:

First, we need to find the apothem of the pentagon. So, the apothem of a regular polygon is equal to:

`a=\frac{s}{2\tan ((180)/(n))_{}}`

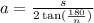
Where s is the length of the sides and n is the number of sides of the polygon.

So, replacing s by 6 in and n by 5, we get:

`\begin{gathered} a=(5)/(2\tan((180)/(5))) \\ a=(5)/(2\tan (36)) \\ a=(5)/(2(0.73)) \\ a=(5)/(1.45)=3.44 \end{gathered}`

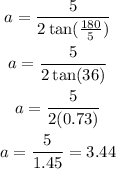
Now, the area of the pentagon will be equal to:

`A=(p* a)/(2)`

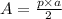
Where p is the perimeter of the pentagon. In this case, the perimeter is equal to:

p = 5 x 6 in = 30 in

Therefore, the area of the pentagon is:

`A=(30*3.44)/(2)=51.6in^2`

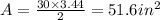
Finally, the volume of the prism will be equal to:

Volume = Area x Height

Volume = 51.6 in² x 18 in

Volume = 928.8 in³