Question

Joy invests a total of $8,500 in two accounts paying 3% and 9% annual interest, respectively. How much was invested in each account if, after one year, the total interest was $705.00.how much was invested at 3% andhow much was invested at 9%.

Answer 1

Let:

x = Amount invested at 3%

y = Amount invested at 9%

Joy invests a total of $8,500, so:

`x+y=8500_{\text{ }}(1)`

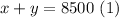
after one year, the total interest was $705.00. so:

`\begin{gathered} I1+I2=705 \\ where \\ I1=0.03x \\ I2=0.09y \\ so\colon \\ 0.03x+0.09y=705_{\text{ }}(2) \end{gathered}`

From (1) solve for x:

`x=8500-y_{\text{ }}(3)`

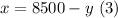
Replace (3) into (2):

`\begin{gathered} 0.03(8500-y)+0.09y=705 \\ 255-0.03y+0.09y=705 \\ 0.06y=450 \\ y=(450)/(0.06) \\ y=7500 \end{gathered}`

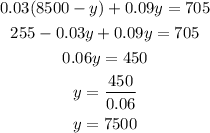
Replace y into (3):

`\begin{gathered} x=8500-7500 \\ x=1000 \end{gathered}`

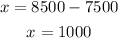
Answer:

$1000 were invested at 3%

$7500 were invested at 9%