Question

A distribution has a mean of 70 and a standard deviation of 8. Ninety-five percent of the distribution can be found between what two numbers? A. 54 and 86 B. 55 and 87 C. 56 and 88 D. 57 and 89.

Answer 1

Step-by-step explanation:

Step 1. The information that we have is:

The mean of the distribution:

`\mu=70`

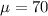
The standard deviation:

`\sigma=8`

and we are required to answer the following question:

Ninety-five percent of the distribution can be found between what two numbers?

Step 2. To solve this problem, we use the empirical rule for the normal distribution.

The rule state the following:

68% of the data will fall under one standard deviation from the mean, 95% of the data will fall under two standard deviations from the mean, and 99.7% of the data will fall under three standard deviations from the mean.

This is best represented in the diagram:

As you can see we have already marked our mean of 70.

Step 3. To find the two numbers, we need to find:

`\begin{gathered} \mu-2\sigma \\ and \\ \mu+2\sigma \end{gathered}`

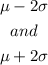
Because 95% of the data will be between those two numbers.

Step 4.

The two numbers are:

`\begin{gathered} \mu-2\sigma=70-2(8)=70-16=54 \\ \mu+2\sigma=70+2(8)=70+16=86 \end{gathered}`

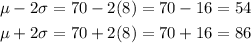
This is represented in the diagram:

Answer:

A. 54 and 86