This question is related to angular frequency of oscillation
Given,
g=10 m/s²
k=80 N/m
m=0.5 kg
A=0.3 m
The angular frequency of oscillation of mass is given by
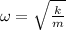
Putting the values in the equation above
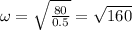
The maximum speed of the mass is given by
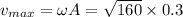
Result: The correct option will be A which is 3.8 m/s