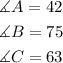Question

7. Find the measure of each angle in AABC. Show your work. B (13x - 3) A 7xº (8x + 15) C

Answer 1

Since interior angles of a triangle adds up to 180 degrees, we can write:

`7x+(13x-3)+(8x+15)=180`

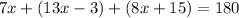
If we clear parenthesis and combine similar terms, we get

`7x+13x+8x-3+15=180`

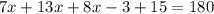
which gives

`28x+12=180`

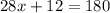
If we move +12 to the right hand side as -12, we obtain

`\begin{gathered} 28x=180-12 \\ 28x=168 \end{gathered}`

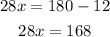
then, x is equal to

`\begin{gathered} x=(168)/(28) \\ x=6 \end{gathered}`

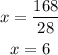
Now, we can substitute this values into each angle

`\begin{gathered} \measuredangle A=7x\Rightarrow\measuredangle A=7(6)=42 \\ \measuredangle B=13x-3\Rightarrow\measuredangle B=13(6)-3=75 \\ \measuredangle C=8x+15\Rightarrow\measuredangle C=8(6)+15=63 \end{gathered}`

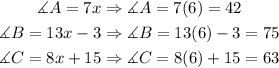
Therefore, the answers are

`\begin{gathered} \measuredangle A=42 \\ \measuredangle B=75 \\ \measuredangle C=63 \end{gathered}`