For two triangles to be similar, their sides must be proportional. We have to choose one of the coordinates to find the sides that are proportional in both triangles.
If we take the coordinates (-3, -2), we end up with three points in a line.
If we take the coordinates (-5, -3), we end up with a not isosceles triangle.
Therefore, these coordinates are not correct in this question.
We now need to find the distance of the last segment D(-3, -1) and E (-3, -5).
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt[]{(-3-(-3))^2+(-5-(-1))^2}](https://img.qammunity.org/2023/formulas/mathematics/college/l2ptd6oxa63p2f1ss9hnygfx29aerbqbzu.png)
![d=\sqrt[]{(-3+3)^2+(-5+1)^2_{}}\Rightarrow d=\sqrt[]{0+16}\Rightarrow d=4](https://img.qammunity.org/2023/formulas/mathematics/college/8jwd55gfr5tarv9d91diysi5lms502eocb.png)
Let us find the distance AC:
![d=\sqrt[]{(0-(-4))^2+(4-2)^2}\Rightarrow d=\sqrt[]{16+4}\Rightarrow d=\sqrt[]{20}](https://img.qammunity.org/2023/formulas/mathematics/college/nlc97rxadtnujd48yt2q8783z4wqv7z22b.png)
The distance AC = CB
The distance AB is:
![d=\sqrt[]{(4-(-4))^2+(2-2)^2}\Rightarrow d=\sqrt[]{8^2}\Rightarrow d=8](https://img.qammunity.org/2023/formulas/mathematics/college/fdm7gefskhajikzhn4kua4nc563uhwtlrk.png)
If we have the coordinates for F (-1, -3), d = sqrt (20). This is the same distance for the previous triangle.
Now, if we take the coordinates (-2, -3), and we follow the same procedure to find the distance, we end up with DF = sqrt (5).
Therefore, if we have:
![(AC)/(DF)=\frac{\sqrt[]{20}}{\sqrt[]{5}}=\sqrt[]{(20)/(5)}=\sqrt[]{4}=2](https://img.qammunity.org/2023/formulas/mathematics/college/x3adf722n29k64z64y1pz63j71pb17vwh9.png)
And
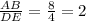
Then, we have that the ratio to the sides is 2, then the coordinates for F is (-2, -3)(last option).