Question

The profit of a company decreased steadily over a ten-year span. The following ordered pairs shows dollars and the number of units sold in hundreds and the profit in thousands of over the ten-year span, (number of units sold, profit) for specific recorded years:(46,1600),(48,1550),(50,1505),(52,1540),(54,1495)Use this tool to find the linear regression line to determine a functionP where the profit in thousands of dollars depends on the number of units sold in hundreds. Share that equation here.Find and interpret the x-intercept.Find and interpret the y-intercept.Use your linear regression to predict when the profit will be $500. To earn full credit for this share all work and calculations used to answer this.

Answer 1

Given the ordered pairs:

(46,1600),(48,1550),(50,1505),(52,1540),(54,1495)

Let's solve for the following.

(a) To find the linear regression line, apply the form:

y = mx + b

Where m is the slope and b is the y-intercept.

To find the slope, m, apply the formula:

`m=\frac{n(\sum ^{}_{}xy)-\sum ^{}_{}x\sum ^{}_{}y}{n(\sum ^{}_{}x^2)-(\sum ^{}_{}x)^2}`

Thus, we have the following:

∑x = 46 + 48 + 50 + 52 + 54 = 250

∑y = 1600 + 1550 + 1505 + 1540 + 1495 = 7690

∑xy = (46*1600) + (48*1550) + (50*1505) + (52*1540) + (54*1495) = 384060

∑x² = 46² + 48² + 50 ² + 52² + 54² = 12540

(∑x)² = 250² = 62500

n = 5

Now, substitute values into the formula and solve for m:

`\begin{gathered} m=(5(384060)-250\ast7690)/(5(12540)-62500) \\ \\ m=-11 \end{gathered}`

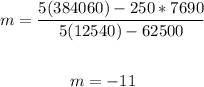
To find the y-intercept, b, apply the formula:

`b=\frac{(\sum ^{}_{}y)(\sum ^{}_{}x^2)-\sum ^{}_{}x\sum ^{}_{}xy}{n(\sum ^{}_{}x^2)-(\sum ^{}_{}x)^2}`

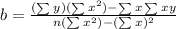
Substitute values:

`\begin{gathered} b=((7690)(12540)-250\ast384060)/(5(12540)-62500) \\ \\ b=2088 \end{gathered}`

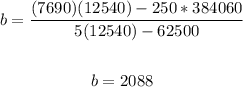
Therefore, the linear regression line to determine a function P where the profit in thousands of dollars depends on the number of units sold in hundreds is:

P = -11n + 2088.

• (2.) To find the x-intercept, substitute 0 for P and solve for n.

We have:

`\begin{gathered} 0=-11n+2088 \\ \\ \text{Add 11n to both sides:} \\ 11n\text{ =-11n+2088} \\ \\ 11n=2088 \\ \\ \text{Divide both sides by 11:} \\ (11n)/(11)=(2088)/(11) \\ \\ n=189.81 \end{gathered}`

The x-intercept is 189.81

This is the point where the company breaks even.

If the company sells 189.81 units the profit will be $0

• (3.) The y-intercept is:

y = 2088

At the beginning of the 10 year span, the profit was $2088

(4). Substitute 500 for P and solve for n.

`\begin{gathered} P=-11n+2088 \\ \\ 500=-11n+2088 \\ \\ \text{Subtract 2088 from both sides:} \\ 500-2088=-11n \\ \\ -1588=-11n \\ \\ \text{Divide both sides -11n:} \\ (-1588)/(-11)=(-11n)/(-11) \\ \\ 144.4=n \\ \\ n=144.4 \end{gathered}`

The profit will be $500 after 144.4 years.

ANSWER:

(1.) P = -11n + 2088

(2.) x-intercept = 189.81

If the company sells 189.81 units the profit will be $0.

(3.) y-intercept = 2088

At the beginning of the 10 year span, the profit was $2088

(4.) The profit will be $500 after 144.4 years.