Let x = amount of time, in min, the slower computer can do the task (on its own)
We can write:
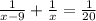
Note: we equated the rates of both. Time and rates are reciprocal of each other.
Let's solve this equation:
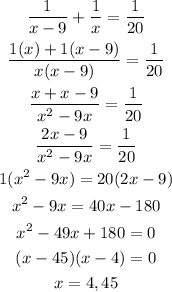
Recall,
x is time of slower computer
x - 9 is time of faster computer
If we take x = 4, "x - 9" becomes negative. So, this solution wouldn't be possible. We take x = 45 as our answer.
So,
faster computer time = x - 9 = 45 - 9 = 36 minutes