Question

A package contains 11 resistors, 2 of which are defective. If 4 are selected find the probability of getting the following results. P(0defectice)

Answer 1

non-defectectiveThe Solution.

Step 1:

We shall determine the number non defectective resistors.

Step 2:

We shall find the probability of defective and non-defective resistors.

Step 3:

We shall find the probability of getting 0 defective when 4 resistors are selected.

Note: Getting 0 defective resistor after 4 selections means that the 4 resistors selected were non-defective resistors. Note also that since the question is silent about replacement, we shall treat it as probability without replacement.

So,

`\begin{gathered} \text{where pr(N}_1)=(9)/(11) \\ pr(N_2)=(8)/(10) \\ pr(N_3)=(7)/(9) \\ pr(N_4)=(6)/(8) \end{gathered}`

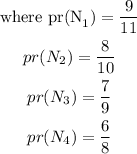
Step 4:

We shall substitute these probabilities and then simplify.

Prob(0 defective resistors) = prob(4 non-defective resistors) =

`\begin{gathered} pr(N_1)* pr(N_2)* pr(N_3)* pr(N_4) \\ =(9)/(11)*(8)/(10)*(7)/(9)*(6)/(8)=(42)/(110) \\ =\text{ 0.38181818 }\approx\text{ 0.381818} \end{gathered}`

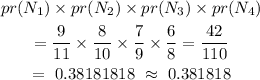
Step 5:

Presentation of the Answer.

So, the probability of getting a 0 defective resistor when 4 resistors are selected is 0.381818

Thus, the correct answer is 0.381818