Question

PQRS is a parallelogram, HSR is a straight line and HPQ = 90°. If |HQ| = 10 cm and |PQ| = 6 cm, what is thearea of the parallelogram?

Answer 1

48 cm²

Explanation:

First, we find the length of HP in the right triangle HPQ using the Pythagorean Theorem.

`\begin{gathered} HQ^2=HP^2+PQ^2 \\ 10^2=HP^2+6^2 \\ HP^2=10^2-6^2=100-36=64 \\ HP^2=8^2 \\ \implies HP=8\text{ cm} \end{gathered}`

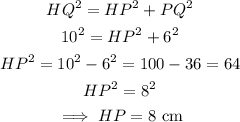
Therefore:

• The height of the parallelogram, HP = 8cm

,

• The base of the parallelogram, PQ = 6m

The area of a parallelogram is calculated using the formula:

`Area=Base* Height`

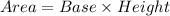
Substitute the values given above:

`Area=6*8=48\;cm^2`

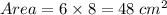
The area of the parallelogram is 48 cm².