Given: The logarithm below
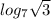
To Determine: The solution of the given
Solution
Using exponent rule below
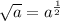
Applying the exponent rule above to the given logarithm
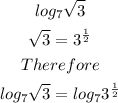
Using logarithm rule to the given

Let us apply change of base as shown below
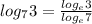
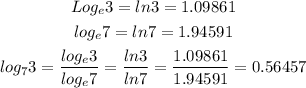
Therefore, we have
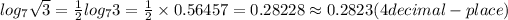
Hence, the final answer is approximately 0.2823