Question

Jake up bought some tickets to see his favorite singer. He bought some adult tickets and some children tickets for a total of nine tickets. The adult ticket cost $10 per ticket and the children’s tickets cost eight dollars per ticket. If he spent a total of $78 then how many adult tickets did he buy

Answer 1

Let the number of adult tickets be

`=x`

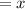
Let the number of children tickets be

`=y`

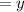
The total number of tickets bought is

`=9`

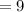
Therefore,

The equation to represent the number of tickets will be

`x+y=78\ldots\ldots\text{.}(1)`

The cost of one adult ticket is

`=10`

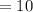
The cost of children's tickets is

`=8`

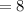
The cost of x number of adult tickets will be

`\begin{gathered} =10* x \\ =10x \end{gathered}`

The cost of y number of children tickets will be

`\begin{gathered} =8* y \\ =8y \end{gathered}`

The total amount spent on the tickets is

`=78`

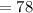
Therefore,

The equation to represent the total amount of money spent will be

`10x+8y=78\ldots\ldots(2)`

Combine the two equations together and then solve simultaneously

`\begin{gathered} x+y=9\ldots\text{.}(1) \\ 10x+8y=78\ldots\ldots(2) \end{gathered}`

Step 1:

Using the elimination method, make x the subject of the formula from equation (1) to form equation (3)

`\begin{gathered} x+y=9 \\ x=9-y\ldots\ldots\text{.}(3) \end{gathered}`

Step 2:

Substitute equation (3) in equation (2) to get the value of y

`\begin{gathered} x=9-y\ldots\ldots\text{.}(3) \\ 10x+8y=78\ldots\ldots(2) \\ 10(9-y)+8y=78 \\ 90-10y+8y=78 \\ -2y=78-90 \\ -2y=-12 \\ \text{Divide both sides by -2} \\ (-2y)/(-2)=(-12)/(-2) \\ y=6 \end{gathered}`

Step 3:

Substitute y=6 in equation (3) to get the value of x

`\begin{gathered} x=9-y \\ x=9-6 \\ x=3 \end{gathered}`

Hence,

The number of adult tickets jake bought = 3