Question

A ship is heading due north at 20 km/h but is blown off course by thewind which is blowing from 30° south west at 5 km/h. What is the speedof the ship, and in which direction is it travelling? Please calculate byalgebraic method.

Answer 1

Given,

The speed of the ship, v=20 km/h due north

The speed of the wind, w=5 km/h

The direction of the wind, θ= 30° southwest

Representing the velocity of the ship in vector form,

`\vec{v}=20\hat{j}`

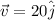
Representing the wind speed in vector form,

`\begin{gathered} \vec{w}=5\cos 30^(\circ)(-\hat{i})+5\sin 30^(\circ)(-\hat{j}) \\ =-4.33\hat{i}-2.5\hat{j} \end{gathered}`

The velocity of the ship after being blown off by wind is,

`\vec{v_0}=\vec{v}+\vec{w}`

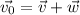
On substituting the known values,

`\begin{gathered} \vec{v_0}=20\hat{j}-4.33\hat{i}-2.5\hat{j} \\ =-4.33\hat{i}+17.5\hat{j} \end{gathered}`

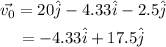
The speed of the ship is the magnitude of vector v₀. Thus the speed of the ship is,

`\begin{gathered} v_0=\sqrt[]{(-4.33)^2+17.5^2} \\ =18.03\text{ km/hr} \end{gathered}`

Thus the speed of the ship after being blown off by the wind is 18.03 km/hr

The direction of the ship is given by,

`\begin{gathered} \theta_0=\tan ^(-1)((17.5)/(-4.33)) \\ =-76.1^(\circ) \end{gathered}`

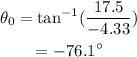
The negative sign indicates the angle is in the clockwise direction.

Thus the direction of the ship is 76.1° north of the west.