Question

Question 9 Alex launched a ball into the air. The height of the ball can be represented by the equation

Answer 1

The height of the ball with respect to time is represented by the following equation

`h(t)=-8t^2+40t+5`

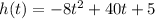
Where h(t) is the height and t is the time in seconds.

Since it is a quadratic equation, let us compare it with the standard form of a quadratic equation.

`f(x)=ax^2+bx+c`

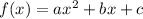
Comparing the given equation with the standard form, the coefficients are

a = -8

b = 40

c = 5

Recall that the x-coordinate of the vertex is given by

`\begin{gathered} -(b)/(2a) \\ -\frac{40}{2(-8)_{}} \\ \frac{40}{16_{}} \\ 2.5 \end{gathered}`

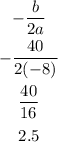
Recall that the y-coordinate of the vertex is given by

`\begin{gathered} h(t)=-8t^2+40t+5 \\ h(2.5)=-8(2.5)^2+40(2.5)+5 \\ h(2.5)=-8(6.25)^{}+100+5 \\ h(2.5)=-50^{}+100+5 \\ h(2.5)=55 \end{gathered}`

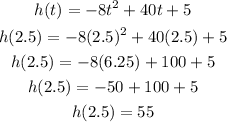
So, the coordinates of the vertex are

`vertex=(2.5,55)`

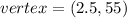
The coordinates of the vertex represent the highest point achieved by the ball.

The vertex tells us that the maximum height of the ball was 55 units and it occurred at 2.5 seconds.

This can be confirmed by looking at the graph of the given equation

As you can see from the above graph, the vertex is the maximum point of the graph that is (2.5, 55)