Question

Graph the line that passes through the points (8,0) and (4,4) and determine the equation of the line.

Answer 1

Concept:

The formula used to calculate the equation of a line when two points are given is given below as

`\begin{gathered} (y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1) \\ \end{gathered}`

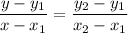
Where the coordinates are given are

`\begin{gathered} (x_1,y_1)\Rightarrow(8,0) \\ (x_2,y_2)\Rightarrow(4,4) \end{gathered}`

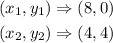
By substituting the values, we will have

`\begin{gathered} (y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1) \\ (y-0)/(x-8)=(4-0)/(4-8) \\ (y)/(x-8)=(4)/(-4) \\ (y)/(x-8)=-1 \\ \text{cross multiply,we will have} \\ y=-1(x-8) \\ y=-x+8 \end{gathered}`

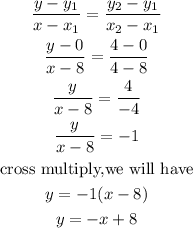
Hence,

The equation of the line is y =-x+8

By graphing the line, we will have the image to be given below as