Question

Find the solution(s) to the system of equations. Select all that apply.y=x^2 - 4y=-2х - 5ОА. (-1, -3)ОВ. (2, 0)ООООС. (-2, 0)оD. (-5, 0)

Answer 1

Given the system of equations:

• y = x² - 4

,

• y = -2x - 5

Let's find the solution(s) to the system.

To find the solution, eliminate the equivalent sides and equate the expressions.

We have:

`x^2-4=-2x-5`

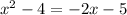
Move all terms to the left and equate to zero.

Add 2x and 5 to both sides:

`\begin{gathered} x^2+2x-4+5=-2x+2x-5+5 \\ \\ x^2+2x+1=0 \end{gathered}`

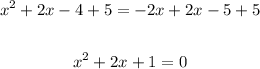
Factor the left side of the equation using the perfect square rule:

`\begin{gathered} x^2+2x+1^2=0 \\ \\ x^2+2\cdot x\cdot1+1^2=0 \\ \\ (x+1)^2=0 \end{gathered}`

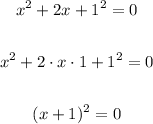
Solving further:

`x+1=0`

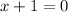
Subtract 1 from both sides:

`\begin{gathered} x+1-1=0-1 \\ \\ x=-1 \end{gathered}`

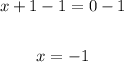
Now, substitute -1 for x in either of the equations and solve for y.

Let's take the first equation:

`\begin{gathered} y=x^2-4 \\ \\ y=-1^2-4 \\ \\ y=1-4 \\ \\ y=-3 \end{gathered}`

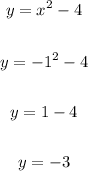
Therefore, we have the solutions:

x = -1, y = -3

In point form:

(x, y) ==> (-1, -3)

ANSWER:

A. (-1, -3)