Question

Solve each of the six equations and decide which category it fits into. You MUST SOLVE before you can do so. One Solution No Solution Infinite Solutions C 1 C :: 4 (k - 8) = -32 + 4k :: 36 - 7p = -7(p-5) :: 8.1 + 38 = 3(-6 - 40) :: 30 + 6p = 7 (P+6) - 5 :: 3+5n = 5(n +2) - 7 :: -2 (0-2) = -3- 20

Answer 1

Let's solve the equations.

1.

`\begin{gathered} 4(k-8)=-32+4k \\ 4k-32=-32+4k \\ 4k-4k=32-32 \\ 0=0 \end{gathered}`

Since by solving the equation we get an equality that always hold the equation has an infinite number of solutions.

2.

`\begin{gathered} 36-7p=-7(p-5) \\ 36-7p=-7p+35 \\ 7p-7p=-36+35 \\ 0=-1 \end{gathered}`

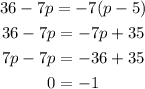
Since this is a contradiction the equation does not have a solution.

3.

`\begin{gathered} 8x+38=-3(-6-4x) \\ 8x+38=18+12x \\ 8x-12x=18-38 \\ -4x=-20 \\ x=(-20)/(-4) \\ x=5 \end{gathered}`

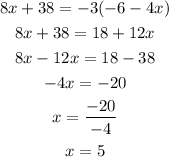
Therefore, this equation has one solution.

4.

`\begin{gathered} 30+6p=7(p+6)-5 \\ 30+6p=7p+48-5 \\ 30+6p=7p+43 \\ 30-43=7p-6p \\ p=-13 \end{gathered}`

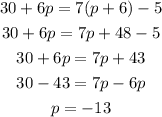
Therefore, this equation has one solution.

5.

`\begin{gathered} 3+5n=5(n+2)-7 \\ 3+5n=5n+10-7 \\ 3+5n=5n+3 \\ 5n-5n=3-3 \\ 0=0 \end{gathered}`

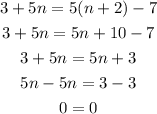
Since by solving the equation we get an equality that always hold the equation has an infinite number of solutions.

6.

`\begin{gathered} -2(v-2)=-3-2v \\ -2v+4=-3-2v \\ 4+3=2v-2v \\ 7=0 \end{gathered}`

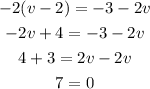
Since this is a contradiction the equation does not have a solution.