Question

Use the above figure and the above formulas to answer the following: What is the distance of AB, BC, and Ad In Triangle ABC Take two? Is Triangle ABC take two a scalene, isosceles, or equilateral? Is triangle ABC take two acute, obtuse, or right?

Answer 1

We are given the following coordinates of points A, B, and C

`\begin{gathered} A(-5,7) \\ B(7,7) \\ C(1,4) \end{gathered}`

Recall that the distance formula is given by

`d=\sqrt{\left( {x_2 - x_1 } \right)^2 + \left( {y_2 - y_1 } \right)^2 }`

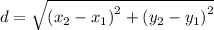
Let us find the distance AB, BC, and AC of the triangle ABC

Distance AB:

A(-5, 7) and B(7, 7)

`(x_1,y_1)=(-5,7)\: \text{and}\: (x_2,y_2)=(7,7)`
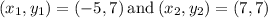
`\begin{gathered} AB=\sqrt[]{({x_2-x_1})^2+({y_2-y_1})^2} \\ AB=\sqrt[]{({7-(-5)_{}})^2+({7_{}-7_{}})^2} \\ AB=\sqrt[]{({7+5})^2+({0_{}})^2} \\ AB=\sqrt[]{({12})^2^{}} \\ AB=12^{} \end{gathered}`

So, the distance AB is 12

Distance BC:

B(7, 7) and (1, 4)

`(x_1,y_1)=(7,7)\: \text{and}\: (x_2,y_2)=(1,4)`
`\begin{gathered} BC=\sqrt[]{({x_2-x_1})^2+({y_2-y_1})^2} \\ BC=\sqrt[]{({1_{}-7_{}})^2+({4_{}-7_{}})^2} \\ BC=\sqrt[]{({-6_{}})^2+({-3_{}})^2} \\ BC=\sqrt[]{36^{}+9^{}} \\ BC=\sqrt[]{45} \end{gathered}`

So, the distance BC is √45

Distance AC:

A(-5, 7) and C(1, 4)

`(x_1,y_1)=(-5,7)\: \text{and}\: (x_2,y_2)=(1,4)`
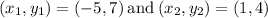
`\begin{gathered} AC=\sqrt[]{({x_2-x_1})^2+({y_2-y_1})^2} \\ AC=\sqrt[]{({1_{}-(-5)_{}})^2+({4_{}-7_{}})^2} \\ AC=\sqrt[]{({1_{}+5})^2+({-3})^2} \\ AC=\sqrt[]{({6})^2+({-3})^2} \\ AC=\sqrt[]{36^{}+9^{}} \\ AC=\sqrt[]{45} \end{gathered}`

So, the distance AC is √45

Is triangle ABC take two a scalene, isosceles, or equilateral?

As you can see, triangle ABC has two equal sides BC and AC

Therefore, triangle ABC is an isosceles triangle.

Is triangle ABC take two acute, obtuse, or right? ​

Let us find out by applying the Pythagorean theorem.

`\begin{gathered} c^2>a^2+b^2 \\ 12^2>(\sqrt[]{45}^{})^2+(\sqrt[]{45}^{})^2 \\ 144^{}>45^{}+45^{} \\ 144>90 \end{gathered}`

As you can see, since the square of the third side is greater than the sum of the squares of the two sides, the triangle ABC must be an obtuse triangle.

An obtuse triangle has one angle greater than 90°

Let us also plot the points on the given graph and draw the triangle ABC to verify the results.

As you can see, the angle ∠C seems to be greater than 90°

Also, the sides BC and AC are equal.

Therefore, the triangle ABC is an isosceles triangle (by side) and obtuse triangle (by angle)