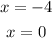Find the equation(s) of the tangent(s) to the circle :2.1. (x + 2 {)}^(2) + {y}^(2) = 4 \: at \: the \: x \: intercepts \: of \: the \: circle

Question

Find the equation(s) of the tangent(s) to the circle :2.1.
`(x + 2 {)}^(2) + {y}^(2) = 4 \: at \: the \: x \: intercepts \: of \: the \: circle`

Answer 1

The equation of a line with slope m that passes through the point (a,b) is:

`y=m(x-a)+b`

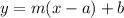
On the other hand, if a curve is defined by a function y=f(x), the line tangent to the curve at a point (a,f(a)) will have a slope equal to f'(a), so the equation of the line tangent to the curve at (a,f(a)) is given by the expression:

`y=f^(\prime)(a)(x-a)+f(a)`

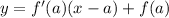
Isolate y from the given equation to find an expression for f(x):

`\begin{gathered} (x+2)^2+y^2=4 \\ \\ \Rightarrow y^2=4-(x+2)^2 \\ \\ \Rightarrow y=\pm√(4-(x+2)^2) \end{gathered}`

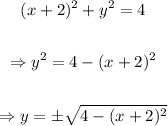
A function must have only 1 value for each input. In this case, y has two possible values for each given value of x. We want to explore the x-intercepts, which are given by the condition y=0. Then, any of the two signs is useful for this purpose. We will choose the positive sign. Then:

`f(x)=√(4-(x+2)^2)`

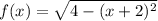
Find the derivative of f:

`\begin{gathered} f^(\prime)(x)=(d)/(dx)f(x) \\ =(d)/(dx)√(4-(x+2)^2) \\ =(1)/(2√(4-(x+2)^2))\cdot(d)/(dx)\left(4-(x+2)^2\right) \\ =(1)/(2√(4-(x+2)^2))\cdot-2(x+2) \\ =-(x+2)/(√(4-(x+2)^2)) \\ \\ \therefore\quad f^(\prime)(x)=-(x+2)/(√(4-(x+2)^2)) \end{gathered}`

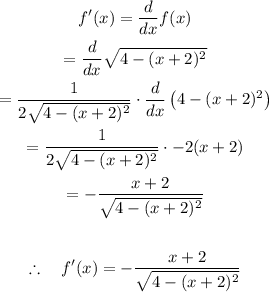
Find the values of x that correspond to y=0:

`\begin{gathered} \left(x+2\right)^2+y^2=4 \\ \Rightarrow\left(x+2\right)^2+0=4 \\ \Rightarrow\left(x+2\right)^2=4 \\ \Rightarrow x+2=\pm√(4) \\ \Rightarrow x+2=\pm2 \\ \Rightarrow x=-2\pm2 \\ \Rightarrow x_1=-4,x_2=0 \end{gathered}`

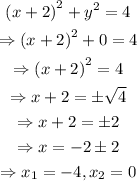
The x-intercepts are -4 and 0, but the denominator of the derivative is equal to 0 when x reaches any of those values, so the derivative diverges.

Then, the slope of the line tangent to the circle at the x-intercepts is not defined, which means that those lines are vertical lines.

Therefore, the equation of the lines tangent to the given circle at the x-intercepts, are:

`\begin{gathered} x=-4 \\ x=0 \end{gathered}`