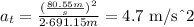(a)
In order to calculate the radial acceleration, use the following formula:
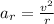
where:
v = 290 km/h
r = 220 m
write the speed in m/s:
290 km/h = 80.55 m/s
replace the values of v and r into the formula for ar:
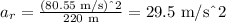
The tangential acceleration can be obtain by using the following formula:
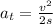
where s is the length of the arc traveled by the car.
s = 2πr/4 = 345.57 m
then, you have: