Question

Find the lateral surface area AND volume of the solid object. Round to nearest whole number

Answer 1

The lateral surface area for the truncated cone or frustum formula is given by

`S_L=\pi(r+R)s`

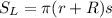
where r is the radius of the upper base, R is the radius of the lower base and s is the slant height. In our case,

`\begin{gathered} r=4.10m \\ R=6.30m \\ s=9.95m \end{gathered}`

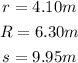
Then, by substituting these values into the formula, we have

`S_L=(3.1416)(4.10+6.30)(9.95)`

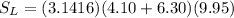
which gives

`S_L=325.09m^2`

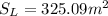
By rounding to the nearest whole number, the lateral surface is equal to 325 square meters.

Now, the volume formula for the frustum is given by

`V=(1)/(3)\pi h(r^2+rR+R^2)`

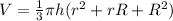
where h is the height, that is, h=9.70 m. Then, by substituting the given values, we have

`V=(1)/(3)(3.1416)(9.70)(4.10^2+(4.10)(6.30)+6.30^2)`

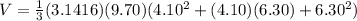
which gives

`V=836.29m^3`

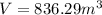
By rounding to the nearest whole number, the volume is 836 cubic meters.