To find:
The value of p for which there are no real solutions.
Solution:
The equation is 2x^2 + px + 4 = 0.
Now, the discriminant of a quadratic equation ax^2 + bx + c = 0 is given by:
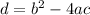
If d < 0, then the equation does not have real solutions. So, for the given equation, there are no real solutions when:
[tex]\begin{gathered} p^2-4(2)(4)<0 \\ p^2<32 \\ -5.65
So, the possible values of p from the given options is -5, 0, 5.
Thus, options B,C,D are correct.