Before we create the equation let's see how it grows, suppose that he starts with 8 villagers, so the first town has 8 villagers and the second town will have 1.17 more, then
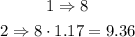
So at the second village, he can have 9.36 villagers, let's round it to 9 villagers, at the third village he can have 1.17 more, but not from 8 villagers, from 9.36 villagers, then
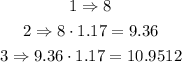
So at the third village, he can have 10.95 villagers, but let's rewrite it to see something interesting, instead of 9.36 let's use 8*1.17, it will help us to create our equation
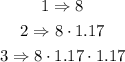
Look that we have 1.17 multiplied two times, so
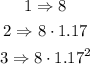
Now let's see the fourth village, it will be the same as the third multiplied by 1.17 again, then
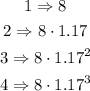
As we can see, we're doing an exponential growing, we can already guess that at the fifth village it will be
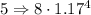
Now we already have the pattern, the generic way to express it will be
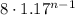
Where "n" is the village, but why (n-1) at the exponential? that's because at the first village (n = 1), we will have
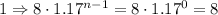
As expected, so we can say that our equation is
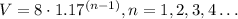
Then to find out the population at the 16th village, let's put n = 16, then
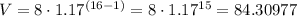
We can round it to 84 villagers.