one function is the inverse of the other

Step-by-step explanation

Step 1
Function Composition is applying one function to the results of another. · (g º f)(x) = g(f(x)), first apply f(), then apply g()
so
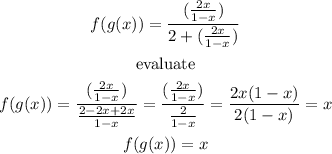
and
Step 2
g(f(x))
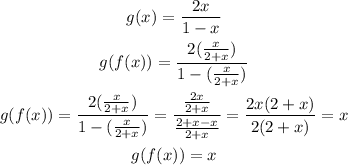
n mathematics, an inverse is a function that serves to “undo” another function. That is, if f(x) produces y, then putting y into the inverse of f produces the output x,
so the realtion between the functios is
one function is the inverse of the other
g is the inverse of f
f is the inverse of g

I hope this helps you