The slant height of cone L=6.3ft
Base radius is5.9/2 =2.95ft
The volume of a cone is given by
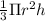
where h= the vertical height of the cone, r=base radius
to find the vertical height, we use Pythagoras theorem
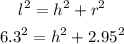
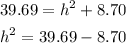
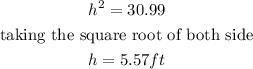
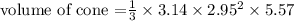
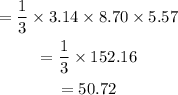
The volume of the cone is 51.0ft³
The right option is the Third one