1 Answer

Navneet Srivastava · Answer 1 · 2023-03-08T23:21:23+0000

Area of a composite figure

The figure consists of a rectangle and a semicircle.

The diameter of the semicircle is the width of the rectangle.

The area of a rectangle of length L and width W is:

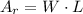
$A_r=W\cdot L$

The given measures are W = 8 and L = 13, thus:

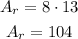
$\begin{gathered} A_r=8\cdot13 \\ A_r=104 \end{gathered}$

The area of a circle of radius r is:

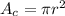
$A_c=\pi r^2$

The area of a semicircle (half a circle) is:

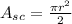
$A_(sc)=(\pi r^2)/(2)$

As mentioned above, the diameter of the semicircle equals the width of the rectangle, thus d = 8

The radius is half the diameter, thus: r = 4. Substituting:

$\begin{gathered} A_(sc)=(\pi\cdot4^2)/(2) \\ \text{Calculating:} \\ A_(sc)=8\pi \\ A_(sc)\approx25.1 \end{gathered}$

The total area is:

A = 104 + 25.1

A = 129.1

Please log in or register to add a comment.