We have two products: a two-slice toaster and a four-slice toaster.
Lets call T the number of two-slice toasters produced and F the number of four-slice toasters produced.
If we have 300 hours per week of labor, the sum of the labor required for T and F has to be lower or equal to that value.
The labor hours that take to make the two-slice toasters can be written as 6*T, as it is the product of the hours per unit (6 hours/unit) by the number of units (T units).
The same can be done for F, where the labor required can be expressed as 10*T.
If we add these terms, and make them be less or equal than 300, we get:
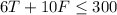
The production capacity is 40 units, so the sum of T and F has to be less or equal than 40.
We can express this as:

Answer:
The system of inequalities for this problem becomes:
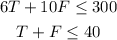
6T+10F<=300
T+F<=40