Question

Antonio has surveyed 21 classmates about the number of credit cards in their wallet and received the following frequency table

Answer 1

We need to first find the probability of P(A) and P(B). These are found by dividing the frequency they appear by the number of surveyed classmates.

`\begin{gathered} P(A)\text{ = }(4)/(21) \\ P(B)\text{ = }(1)/(21) \end{gathered}`

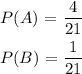
We can now calculate the probabilities the problem asks for. When we need to calculate the probability of two events happening at the same time, we express it as P(A and B). In this cases we need to multiply the individual probabilities, in this case we need to multiply P(A) to P(B). Since they're fractions we need to multiply the numerator of one by the numerator of the other, while we multiply the denominator of one to the denominator of the other.

`\begin{gathered} P(A\text{ and B) = P(A)}\cdot P(B) \\ P(A\text{ and B) = }(4)/(21)\cdot(1)/(21) \\ P(A\text{ and B) = }(4)/(441) \end{gathered}`

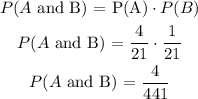
We now need to find the value of the probability of P(A or B). In cases where the two events are independent, that means that they are mutually exclusive, if one happens the other won't, we need to sum the individual probabilities. This case is mutually exclusive, if the classmate has 4 credit cards in his wallet he won't have 1, therefore we can sum the probabilities. Since they are fractions with the same denominator we can simply mantain the denominator and sum the numerators.

`\begin{gathered} P(A\text{ or B ) = P(A) + P(B)} \\ P(A\text{ or B) = }(4)/(21)+(1)/(21)\text{ = }(5)/(21) \end{gathered}`

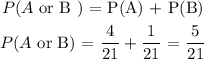
Since the events are mutually exclusive we don't need to subtract the probability of both happening at the same time.