Final Answer:
1. The graph of
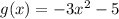 is a downward-facing parabola, reflecting a vertical stretch by a factor of 3 and a vertical translation downward by 5 units compared to the graph of
is a downward-facing parabola, reflecting a vertical stretch by a factor of 3 and a vertical translation downward by 5 units compared to the graph of
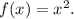
Step-by-step explanation:
The function
 represents a standard upward-facing parabola with its vertex at the origin. The given function
represents a standard upward-facing parabola with its vertex at the origin. The given function
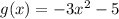 is a transformation of
is a transformation of
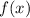 . The coefficient -3 indicates a vertical stretch by a factor of 3, causing the parabola to open downward. The constant term -5 represents a vertical translation downward by 5 units.
. The coefficient -3 indicates a vertical stretch by a factor of 3, causing the parabola to open downward. The constant term -5 represents a vertical translation downward by 5 units.
To understand the transformation, consider specific points. For instance, when
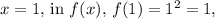 and in
and in
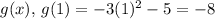 . This demonstrates the vertical stretch and translation in action.
. This demonstrates the vertical stretch and translation in action.
The negative coefficient in
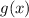 reflects the parabola's orientation, making it open downward. The vertical stretch by a factor of 3 amplifies the steepness of the graph, and the downward translation shifts the entire graph lower. Therefore, the comparison between the graphs of
reflects the parabola's orientation, making it open downward. The vertical stretch by a factor of 3 amplifies the steepness of the graph, and the downward translation shifts the entire graph lower. Therefore, the comparison between the graphs of
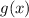 and
and
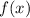 indicates a transformed parabola that is wider, steeper, and shifted downward.
indicates a transformed parabola that is wider, steeper, and shifted downward.